[ Article ]

GRI REVIEW - Vol. 20, No. 4, pp.153-172

ISSN: 2005-8349 (Print)

Print publication date 30 Nov 2018

Received 08 Oct 2018 Revised 26 Oct 2018 Accepted 01 Nov 2018

캐놀라 선물시장에서의 거래행위와 시장효율성

이상훈^**

**경기연구원 상생경제연구실 선임연구위원

Trading Behavior and Market Efficiency in Canola Futures Market

Sanghoon Lee^**

**Senior Economist, Department of Sustainable Economy, Gyeonggi Research Institute, Korea

초록

본 연구의 목적은 캐놀라 선물시장 참여자들의 일일 거래행위에 행위 패턴의 존재여부를 분석하여 시장의 효율성을 판단하려 하였다. 시장에서 일정한 행위 패턴이 있을 경우 시장은 비효율적인 것으로 판단할 수 있으며 주요 연구결과는 다음과 같다. 첫째, 캐놀라 선물시장에서 가격이 하락할 경우와 상승할 경우 거래행위에서 일정한 패턴이 존재한다. 둘째, 이러한 패턴은 계약월과 연도에 따라 95% 신뢰구간에서 서로 다르게 나타났다. 비모수 분석의 경우에도 계약월과 연도에 따라 모수분석의 경우와 같은 수준의 패턴을 보였다. 이러한 결과는 시장행위를 나타내는 일부 데이터에서 비정규분포의 가능성이 있지만 선물시장의 데이터가 전반적으로 정규분포의 형태를 이루고 있음을 뜻한다. 결론적으로, 본 연구결과는 선물시장에서의 가격 변동은 시장참여자들의 행위의 결과이고, 이러한 행위는 어느 정도 예측 가능하여 효율적인 예측시스템을 갖출 수 있음을 보였다.

Abstract

The objective of this study was to test the pattern of daily trading behavior and to test the efficiency in futures market. First, the results showed the existence of patterns in daily trading behavior in declining and rising canola futures markets. Second, these patterns were different across the different year and contract in the 95% significance level. Nonparametric approach showed the same level of predictive patterns of trading behavior across the year and the contract. This showed normal distribution of market behavior in spite of some possibility of non-normal distribution in certain contracts. Finally, this study proved in some how the facts that price movement in the futures market are the result of market participants’ actions and could be predictable. Thus, we need to emphasize the existence of structures as efficient forecasting tools and systems when some predictable rules for market participants’ daily activities exist.

Keywords:

discriminant analysis, futures price pattern, market efficiency

키워드:

판별분석법, 선물시장 가격패턴, 시장효율성

Ⅰ. 서 론

선물시장과 관련된 주요 가설 중의 하나는 ‘시장의 효율성’에 관한 것이다. 시장이 완전하게 효율적일 경우 선물가격은 항상 균형점에 이르고 가격 변동패턴 또한 무작위의 경향을 보인다. 따라서 이 경우 가격패턴과 시장상황을 통한 선물시장 가격 예측은 무의미 하다. 반면, 선물시장이 완전하게 효율적이지 않을 경우 메모리 또는 패턴이 존재하고 과거의 가격 자료를 활용한 가격 예측은 일정부분 가능할 수 있다. 이러한 시장의 효율성에대한 판단은 가격결정과정의 일관성과 시계열적 상관성 정도를 분석하여 확인할 수 있다. 만일 선물가격의 변동과정에서 시계열적 상관성 또는 어떤 패턴이 발견된다면, 시장이 효율적이라는 가설은 제거될 수 있다. 다시 표현하면, 선물시장가격이 원칙이 없이 균형점으로 움직이는 무작위성의 가설이 제거되고, 패턴에 대한 분석을 통해 어느 정도 예측 가능성이 있음을 의미한다.

선물시장의 시장효율성과 관련된 이전의 선행연구 결과는 서로 상반된 결과를 보여준다.

Goldenberg(1989)는 선물시장의 가격 변동이 메모리를 가지고 있지 않기 때문에, 현재의 시장가격이 과거의 시장가격 시리즈와의 연관성을 보여주는 구조적인 패턴을 가지고 있지 않다고 결론지었다. 또한, Fung과 Lo(1993)는 유로달러와 재정채권 선물에서의 장기간 메모리가 있는지 여부를 테스트하였다. 이들은 결론적으로 선물가격은 일일가격, 주간가격, 월간가격 등에서 메모리가 없음을 밝혀 미약하나마 효율적인 시장 가설을 지지하는 연구결과를 제시하였다.

반면, 선물시장가격이 장기간에 걸쳐 가격행태와 구조를 가지고 있다는 연구결과도 있다. Helms과 Kaen, Rosenman(1984)는 상품선물시장 가격과 이전의 가격 변동과의 연관성 여부를 분석하였다. 그들의 결과는 대두와 대두오일, 대두박 선물에서의 일일가격 변동에 과거 가격과의 영속적인 연관성이 있음을 보였다. Martell과 Trevino(1990)는 밀과 옥수수, 대두선물에서 가격행위의 동질성(일관성)여부를 분석하였다. 그들은 일간(intraday) 가격행위는 동질적이지 않고, 다만, 해당선물의 거래기간 동안 일간의 시계열 상관성은 작은 규모에서 때로는 크게 역방향(negative)으로 변함을 발견하였다. DeCoster와 Labys, Mitchell(1992) 등은 상관성면 테크닉(the correlation dimension technique)을 활용하여 설탕,커피, 은, 구리의 일일(daily) 선물에서 불규칙한 구조의 존재 여부를 확인하였다. 그들의 연구결과는 데이터 내에 특히 비선형 형태의 구조가 있음을 보였다. Olszewski(1998)는 농산물선물을 포함하여 10개 선물에서의 시장의 비효율성 여부를 확인하였고, 선물시장에 비효율성의 증거가 어느 정도 있다고 결론지었다. 이러한 시장 비효율성 때문에 시장 모맨텀과 장기간의 메모리 의존성에 근거한 추세치 반영 거래시스템이 이윤을 남길 수 있다고 판단하였다.

한편, 시장의 효율성에 대한 다른 연구에서는 효율적인 시장과 비효율적인 시장의 증거를 동시에 보여주고 있다. Kamara(1982)는 선물가격 변동의 무작위적(random walk) 성향을 분석하였다. 분석결과 어느 정도의 시계열적 상관성을 발견하였지만, 이들 결과는 분석방법과 분석에 이용한 표본자료 기간에 크게 영향을 받는다는 사실을 보여주었다. Kawaller와 Koch, Peterson(1994)은 분명한 과거 변동성의 일일가격 패턴을 발견하였지만, 유로달러 선물과 S&P 500지수 선물, 독일 마르크 선물, 생가축선물에서는 분석적으로 분명한 패턴은 발견되지 않았다. Corazza와 Malliaris, Nardelli(1997)는 6개의 농산물 선물가격 행태를 실증적으로 분석하여 임의성 문제와 로그 정규분포 여부를 테스트하였다. 그들은 시장효율성은 특수한 이론이며 일반적인 이론은 아니라고 결론지었다. 때로는 효율적이지만 다른 경우는 효율적이지 않다는 것이다. 따라서 임의성(randomness)과 시장효율성 가설을 제거하기에 충분치 않다는 결론을 냈다.

최근 선물시장의 효율성에 관한 연구는 다양한 분석형태로 지속적으로 이루어지고 있다.Westerlund(2013) 등은 금, 은, 플래티늄 등의 상품 선물시장에서 효율적 시장 가설을 검증하려 하였다.이들은 현물 및 선물가격의 변동은 시장에서 상호 연관되어 동행성을 보여주지만, 원유시장은 결과가 다르게 나타남을 보였다. 또한, 선물시장이 이분산적(heteroskedastic)시장이기 때문에 최소제곱법(OLS)에 의한 연구결과가 효과적이지 못하다고 주장하였다. Bosch(2016) 등은 선물시장에서 위험분산거래자(hedger), 투기자(speculator), 상품지수 거래자 등 다른 유형의 시장거래자들이 어떻게 시장가격에 영향을 주는가를 분석하였다. 그들은 상품지수 선물에서 투기자들의 거래행위가 현물시장 가격과 선물시장 가격의 차이를 감소시키는 강한 증거를 발견하였다. 그 외 Jiang(2011) 등은 1988∼2007년 기간 동안 S&P 500 지수 옵션시장에서 효율적 시장 가설과 정보전달 면에서의 효율성을 검증하려 시도하였다. 그들의 결론은 전반적으로 옵션시장에서 가격 변동의 임의성과 정보의 효율성이 있다는 결론을 내렸다. 이상의 결과를 보면 시장 효율성을 검증하려는 다양한 시도가 진행되고 있음을 알 수 있다. 대부분의 경우 이윤을 발생시킬 수 있는 어떤 패턴이나 상관성을 발견하려 하고, 이러한 결과를 비효율적인 시장의 증거로 여기려는 시도를 하였다.

본 연구에서는 기존연구와 다르게 분석도구로서 다변량분석법(multivariate method) 중 판별분석법(discriminant analysis method)이 활용되었다. 판별분석법이 회귀분석과 다른 점은 종속변수가 연속적이지 않고 확률적으로 특정 모집단(카테고리)으로 분류할(categorical) 수 있다는 점이다. 즉, 기존의 알려진 정보를 활용하여 예측시스템을 만들 수 있고, 예측시스템에 의해 새로운 관찰치를 특정 그룹으로 분류해 내는 분석 방법이다. 본 연구에서 판별분석법은 캐놀라 선물거래에서 나타나는 변수간의 함수관계에 의한 승수와 상관성의 도출에 의존하지 않고, 누적된 거래 행위 자료의 모양(shape)을 통해 가격변동 여부를 확률적으로 예측하도록 응용되었다는데 의미가 있다.

가격 변동에 대한 예측력은 판별분류법칙에 의해서 분류된 결과와 실제상황과 비교함으로써 예측력을 확률적으로 계산할 수 있다. 즉, 가격자료를 포함, 이미 알고 있는 과거의 거래 자료를 활용하여 3개 그룹(가격상승, 가격하락, 가격불변 등) 모집단으로 분류를 하고, 신규 표본에 대해 이들 3개 그룹 중 어느 그룹으로 분류할 것인가를 확률적으로 예측한 결과와 실제결과를 비교하여 정확도를 판단하고 정확도가 높을 경우 시장참여자들의 거래행위가 일정하게 반복된다고 판단하였다. 시장참여자들의 일일 행위로부터 예측할 수 있는 일정한 법칙을 발견할 수 있다면, 시장은 비효율적이라는 결론을 도출할 수 있다.

본 연구의 구성은 다음과 같다. 제2장에서는 분석모형의 설정과 함께 분석과정을 설명하였다. 제3장에서는 분석자료를 기술하며, 제4장 및 제5장에서는 분석결과와 함께 본 연구의 결론을 정리하였다.

Ⅱ. 분석모형의 설정

1. 판별분류법칙(Discriminant Classification Rule)의 응용

캐놀라 선물거래에서 일일 종장가격의 방향을 나타내는 모집단은 3개 그룹으로 분류할 수 있으며 이는 전일대비 가격이 하락한 그룹, 가격이 상승한 그룹, 그리고 가격이 불변한 그룹으로 구분될 수 있다. 이들 모집단이 각각 다변량 정규분포(multivariate normal distribution)를 이루고 있다면, 가격 하락그룹은 $Π 1 ∼ N μ 1, Σ 1$ , 가격 상승그룹은 $Π 2 ∼ N μ 2, Σ 2$ , 그리고 가격 불변 그룹은 $Π 3 ∼ N μ 3, Σ 3$ 으로 나타낼 수 있다.

선물시장에서 새로운 관찰치를 나타내는 표본 데이터 그룹인 벡터 x가 있고 x를 3개 모집단 중 하나로 분류시켜야 한다면, x가 3개 그룹 중 가장 유사한 그룹으로 분류될 수 있도록 예측할 수 있는 판별분류 법칙을 개발할 수 있다. 여기서 표본 데이터 그룹 벡터 x는 개장가격(open), 최고가격(high), 최저가격(low), 거래량(volume), 그리고 미청산계약고(open interest) 등 시장 참여자들의 행위를 나타내고 있고, 판별을 위해서 다음과 같은 법칙을 이용할 수 있다.

1) 우도(Likelihood) 법칙

판별분류법칙 중 고려할 수 있는 법칙 중 우도법칙(Likelihood rule)은 다음과 같이 표현될 수 있다.

선택 Π i, 만일 L x; μ i, Σ i > L x; μ j, Σ j for i ≠ j = 1,2, 3 단, μ i : i 번째 모집단의 평균벡터 Σ i : i 번째 모집단의 분산 - 공분산 행렬 L x; μ i, Σ i : x 에서 평가되는 i 번 째 모집단의 우도함수 (likelihood function), i = 1,2, 3 (가격 하락, 가격 상승, 가격 불변)

식 (1)

이 경우 표본 데이터 그룹 는 3개 모집단 중 우도함수가 가장 크게 나타나는 그룹 $Π i$ 로 새로운 관찰치 x를 분류한다.

2) 마할라노비스(Mahalanobis) 제곱거리 법칙

가격 하락, 가격 상승, 가격 불변의 3개 모집단이 동일한 분산-공분산 행렬 $Σ 1 = Σ 2 = Σ 3$ 을 가지고 있다면, 우도법칙(likelihood rule)은 또한 다음과 같이 표현될 수 있다.

선 택 Π i, 만 일 d i 2 < d j 2 인 경 우 단, = d i 2 = x - μ i' Σ - 1 x - μ i for i ≠ j = 1,2, 3

식 (2)

여기서 $d i 2$ 은 벡터 x가 $μ i$ 로부터 얼마나 떨어져 있는가를 나타내는 거리의 측정치로서 $d i 2$ 는 $i = 1,2, 3$ 인 상태에서 x와 $μ i$ 사이의 마할라노비스 제곱거리라고 불린다. 마할라노비스 제곱거리 법칙은 평균벡터가 가장 근접한 모집단으로 새로운 관찰치 벡터 x를 분류하는 방식이다.

3) 베이즈(Bayes) 분류법칙

분류결과에 대한 사전정보가 있을 경우, $P i$ 를 $i$ 그룹의 사전확률이라 하고, 무작위적으로 추출한 관찰치가 모집단 $Π i$ , $i = 1,2, 3$ (가격하락, 가격상승, 가격불변)에서 왔을 확률이라 하자. 또한, $C i / j$ 는 새로운 관찰치를 모집단 $Π j$ 에서 모집단 $Π i$ 로 잘못 분류함에 따른 비용을 나타내고, $P i / j$ 는 새로운 관찰치를 모집단 $Π j$ 에서 모집단 $Π i$ 로 잘못 분류할 확률이라 할 경우, 무작위적으로 선택한 관찰치가 잘못 분류됨에 따른 평균비용은 다음과 같이 표현될 수 있다.

P i ⋅ C j / i ⋅ P j / i + P j ⋅ C i / j ⋅ P i / j for i ≠ j = 1,2, 3

식 (3)

이와 같이 3개 각각의 모집단에 대하여 사전확률이 P₁, P₂, P₃로 주어진 상태에서, 무작위로 선택된 관찰치가 잘못 분류되어 발생하는 평균비용을 최소화 하도록 벡터 를 분류하도록 설정된 법칙을 베이즈(Bayes) 판별법칙이라 한다. 이 경우, 판별분류법칙(DCR)은 다음과 같이 표현될 수 있다.

선택 Π i, 만일 P j ⋅ f j x; θ j ⋅ C i / j < P i ⋅ f i x; θ i ⋅ C j / i for i ≠ j = 1,2, 3

식 (4)

여기서 $Π 1, Π 2, Π 3$ 가 다변량 정규분포를 이루는 모집단일 경우, 베이즈 법칙은 다음과 같이 표현될 수 있다. 를 최소화시키는 $d i 2$ 를 $Π i$ 선택한다.

단, d i 2 = x - μ i' Σ - 1 x - μ i + l o g ⁡ Σ i - 2 l o g P i ⋅ C j / i for i ≠ j = 1,2, 3

식 (5)

만일 $Π 1, Π 2, Π 3$ 가 동일한 분산-공분산 행렬을 이루고 다변량 정규분포를 이루는 모집단일 경우 베이즈 법칙은 다음과 같이 표현된다.

$d i 2$ 를 최소화시키는 $Π i$ 를 선택한다.

단, d i 2 = x - μ i' Σ - 1 x - μ i - 2 l o g P i ⋅ C j / i for i ≠ j = 1,2, 3

식 (6)

여기서, 가격 변화 방향을 나타내는 3개 방향으로 잘못 분류시킬 오류 비용과 분산-공분산 행렬이 동일할 경우, $i$ 번째 그룹의 분류함수(classification function)는 다음과 같이 정의되고, $d i 2$ 를 최소화시키는 함수로 정의된다.

d i 2 = x - μ i' Σ - 1 x - μ i - 2 l o g P i for i ≠ j = 1,2, 3

식 (7)

4) 최근접 이웃을 선정하는 비모수 판별분류법칙(Nonparametric Nearest Neighbor DCR)

비모수 분석법에서 판별분류법칙은 모집단이 정규분포일 필요가 없다. 3개 모집단 중 하나로 분류시킬 예정인 새로운 관찰치 벡터 x에 대해 다음과 같은 과정을 거치는 바, 우선, 측정을 위한 일련의 데이터 세트에서 새로운 관찰치 벡터 에 대해 가장 근접한 관찰치 그룹을 찾아 포함시킨다. 즉, 마할라노비스 거리가 가장 작은 관찰치를 찾아 해당 모집단으로 분류시켜, 관찰치 그룹의 최근접 거리의 이웃이 있을 때, x를 해당 그룹에 배속시키는 방식이다. 이러한 방법으로 새로운 관찰치의 k번째 근접 이웃을 찾는 과정이 지속되고, 새로운 관찰치가 k번째 이웃이 속한 그룹으로 배속시키는 과정은 그룹화가 종료될 때까지 지속된다.

Ⅲ. 분석자료 및 실증분석 과정

1. 분석자료

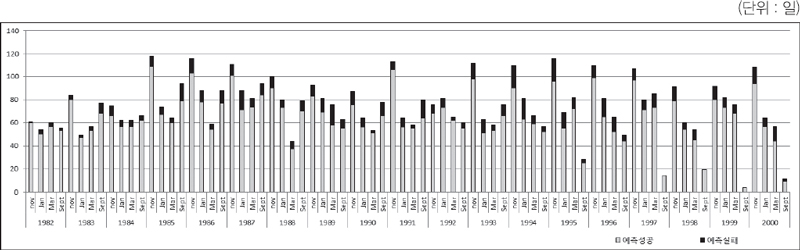
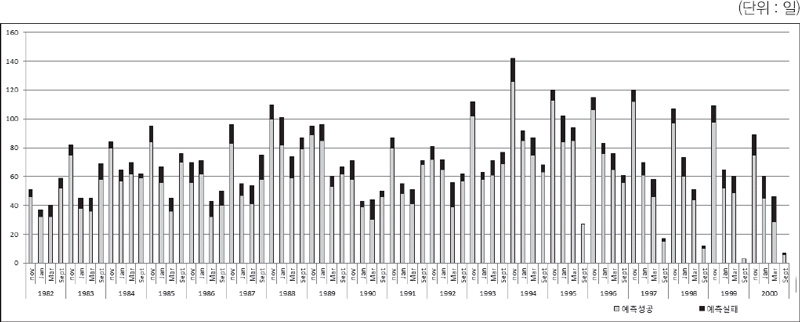
본 연구에서는 캐놀라¹⁾ 선물(canola futures) 가격을 분석대상으로 하였다. 분석에 활용된 선물 시장가격은 1982년∼2000년 기간 동안 캐나다 위니펙선물거래소(WCE: Winnipeg Commodity Exchange) 의 캐놀라(canola) 선물가격이며, 위니펙 거래소가 ICE(Intercontinental Exchange)²⁾ 에 통합된 이후 2010년∼2016년까지는 ICE 캐놀라 선물가격 자료를 활용하였다. 위니펙(WCE)선물거래소와 인터컨티넨탈거래소(ICE)의 캐놀라 선물거래에서 1월물, 3월물, 5월물, 9월물 또는 7월물 등 4개 계약월의 일일종장가격의 방향(상승, 하락, 평행이동)이 자료로 분석에 활용되었다³⁾.

분석과정에서 활용된 선물거래 관련 자료는 실제 거래된 일(daily) 자료로서 각 계약월별로 분석기간동안 거래된 자료이다. 선물시장 거래에 대한 분석에서 가격 자료에 대해 표본을 활용할 경우, 특정기간 특별한 상황이 반영된 상태에서 분석결과와 해석이 다를 수 있다고 판단하였고, 본 연구는 이러한 문제를 해결하기 위해 표본자료가 아닌 실제 거래관련 모집단의 전수 자료를 활용하였다.

본 분석에서는 시장 거래자들의 행위가 현재와 과거의 가격, 거래 기간 동안의 거래량, 미청산계약고 등으로 나타나기 때문에, 거래 참여자의 일일 거래행위는 개장(open)가격, 최고(high)가격, 최저(low)가격, 종장(closing)가격, 거래량(volume), 미청산계약고(open interest)로 표현되는 것으로 판단하였다. 이러한 과거의 일일 거래행위는 당일의 종장가격의 방향을 결정하여 전일의 종장가격대비 상승하였는가, 하락하였는가, 아니면 평행 이동하였는가를 결정할 것이다. 여기에, 다변량 정규분포를 나타내는 3개 모집단, 즉, 하락그룹 모집단, 상승그룹 모집단, 평행이동 그룹모집단으로 구분하였다. 캐놀라 선물시장에서의 거래행위를 나타내는 다양한 데이터의 누적적인 자료를 이용하여 가격 방향을 예측할 수 있다면, 시장이 비효율적이고 가격 예측도 가능하다는 결론을 내릴 수 있을 것이다.

2. 분석 과정

본 연구의 데이터 분석과정에서는 SAS 패키지를 활용하여 판별분석이 이루어졌고 통계적 검정과정도 이루어졌다. 캐놀라 선물가격 자료의 연도별 시계열성을 해소하고, 위니펙 거래소에서 ICE 거래소로 운영이 바뀌면서 발생할 수 있는 영향을 최소화하기 위해 2001년∼2009년의 9년간 기간을 분석에서 제외시켰다. 또한, 판별력이 있는 효율적인 변수를 선정하기 위해, 11월물을 대상으로 SAS를 이용한 변수선별과정(stepwise)이 진행되었다. 이러한 과정은 판별력이 높은 변수를 선정하기 위한 유용한 사전적방법으로서 11개 변수에서 출발을 하여, 진입을 위한 유의수준 0.4, 잔존을 위한 유의수준 0.1을 적용, 8개 변수를 최종적으로 선정하였다.

11개 변수는 전일의 개장가격(open(t-1)), 전일 최고가격(high(t-1)), 전일 최저가격(low(t-1)), 전일 종장가격(closing(t-1)), 전일의 미청산계약고(open interest(t-1)), 전일 거래량(volume(t-1)), 당일 개장가격(open(t)), 당일 최고가격(high(t)), 당일 최저가격(low(t)), 당일 미청산계약고(openinterest(t)), 그리고 당일 거래량(volume(t))이다. 최종적으로 전일 개장가격(open(t-1)), 전일 종장가격(closing(t-1)), 전일의 미청산계약고(open interest(t-1)), 전일 거래량(volume(t-1)), 당일 개장가격(open(t)), 당일 최고가격(high(t)), 당일 최저가격(low(t)), 당일 거래량(volume(t))이 포함되었다.

이들 8개 변수가 1월물과 3월물, 9월물, 11월물에 대해 1982년 이후 2000년 기간 동안 가격 방향 예측에 활용되었고, 2010년 이후 2016년까지는 1월물, 3월물, 7월물, 11월 물에 대한 분석이 이루어졌다. 3개 다른 그룹을 위한 사전확률은 가격 하락확률 49.5%, 가격 상승확률 49.5%, 그리고 가격이 불변할 확률은 1%로 주어졌다. 이 경우 t기의 판별분류법칙은 다음과 같이 표현된다.

DCR ⁡ t = o p e n t - 1 + closing ⁡ t - 1 + v o l u m e t - 1 + o p e n i n t e r e s t t - 1 + o p e n t + h i g h t + l o w t + v o l u m e (t)

식 (8)

단, i : 가격 하락, 가격 상승, 가격 불변
t : 당일
t-1: 전일

다른 표현으로 나타내면 판별분류법칙 DCR $i$ (t)은 $d i 2$ 를 최소화시키는 방식으로 그룹 $i$ 를 결정한다.

$d i 2 = x - μ i Σ - 1 x - μ i - 2 l o g ⁡ (P i) for i ≠ j = 1,2, 3$

단, x : 관찰치 벡터[open(t-1), closing(t-1), volume(t-1), open interest(t-1), open(t), high(t), low(t), volume(t)]

$μ i$ : 모집단 그룹 $i$ 에서 x의 평균 벡터

$P i$ : 모집단 그룹의 사전확률

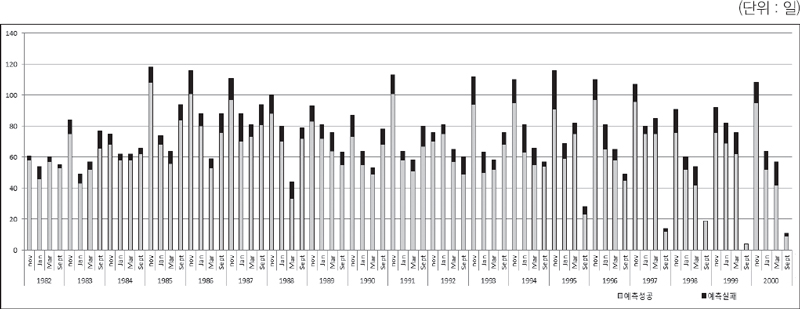
1982년 이후 2000년도까지 19년 기간 동안, 베이즈(Bayes) 법칙을 고려, 매년 4개의 계약월(1월물, 3월물, 9월물, 11월물)에 대한 판별분류법칙(DCR)이 개발되었다. 이렇게 개발된 판별분류법칙을 이용하여 매년 1월물, 3월물, 9월물, 11월물에 대해 판별분석을 하였고 판별분류법칙(DCR)에 의해 예측한 결과와 실제 결과가 사후적으로 비교되었다. 즉, 1월물에 대해서 19년 기간 동안 19번의 판별분류법칙이 개발되어 가격변동상황이 예측되었고 나머지 3월물, 9월물, 11월물에 대해서도 동일하게 19년 기간 동안 19회에 걸쳐 판별분류법칙이 개발되어 활용되었다. 19년 기간 동안 4개 계약월에 대해 판별분석이 이루어져 총 76회 판별분석이 이루어 졌다. 판별분류법칙에 의해 예측된 일일 가격변동은 실제 일일 가격변동과 비교되어 정확한 예측 여부를 분석하였다.

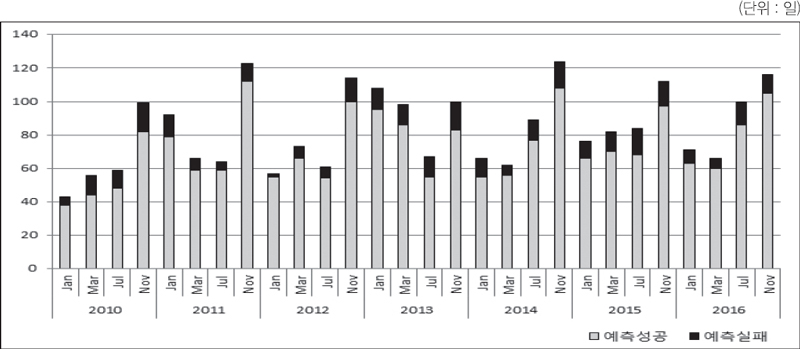
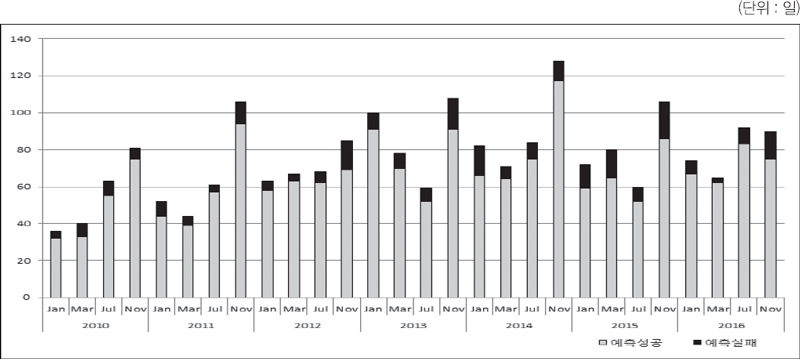
한편, 2010년∼2016년 기간 동안에도 4개의 계약월(1월물, 3월물, 7월물, 11월물)에 대해 각각 매년 판별분류법칙(DCR)이 개발되었고, 개발된 판별분류법칙을 이용하여 일일 가격방향에 대한 예측이 매년 이루어졌다. 이 기간 동안에는 9월물이 ICE 거래소의 상장에서 제외되어 7월물에 대해 분석을 하였다. 동일한 방법으로 4개 계약월(contracts)에 대한 판별분석이 매년 이루어졌으며, 7년 기간 동안 4개 계약월로 총 28회의 판별분석이 진행되었다.

이러한 과정을 통해 나타난 판별분류의 결과는 각각의 그룹, 즉 가격 하락, 가격 상승, 가격 불변의 경우로 나뉘어져서 다른 계약월(contracts)과 해당 연도(years)의 결과와 비교되었다. 계약월(contracts)과 해당연도(years), 가격 방향(directions)이 각각 다른 경우, 결과에서 예측력의 동질성(homogeneity)여부가 통계적 유의수준으로 검증되었다. 검증내용은 첫째, 거래행위가 일관성을 유지하여 축적된 행위정보를 통해 확률적으로 가격 변동을 예측할 수 있는가 여부이고, 둘째, 이러한 행위는 상품(commodity)과 계약월(contract), 기간(period)에 관계없이 동일한가 여부를 판단하는 것이다.

Ⅳ. 분석 결과

1. 모수(Parametric) 분석결과

1) 1982∼2000년 기간

위니펙 선물거래소에서 1982년 이후 2000년까지 19년 기간 동안 캐놀라 선물 거래일은 총 10,998일이며, 총 거래일 10,998일 중에서 종장가격이 전일에 비해 하락한 일은 5,543일이며 상승한 경우는 5,291일, 가격불변인 경우는 183일이다. 베이즈(Bayes) 판별분류법칙(DCR)은 4,917일을 가격 하락으로 분류를 하였고, 4,613일을 가격 상승으로, 그리고 가격 불변은 8일로 예측하였다. 경험적으로 종장가격이 전일 대비 불변인 경우는 매우 드믄 경우로 예측결과에 나타났다. 판별분류법칙은 종합적으로 가격 하락시 88.7%의 정확한 예측을, 가격 상승시 87.2%의 정확한 예측을 그리고 가격 불변시 4.4%의 예측력을 보였다 .

<표 1>

모수 Bayes DCR에 의한 예측결과 종합(1982〜2000)

이상의 분석결과를 종합하면 캐놀라 선물시장에서 시장참여자들의 거래행위에 일정 패턴구조가 있고, 이러한 패턴구조는 전일의 상황이 당일의 가격 예측에 반영되어 상대적으로 높은 예측력을 보이고 있는 것으로 해석된다.

<그림 1>

모수 Bayes DCR에 의한 연도별 가격 하락 예측결과(1982〜2000)

<그림 2>

모수 Bayes DCR에 의한 연도별 가격 상승 예측결과(1982〜2000)

2) 2010∼2016년 기간

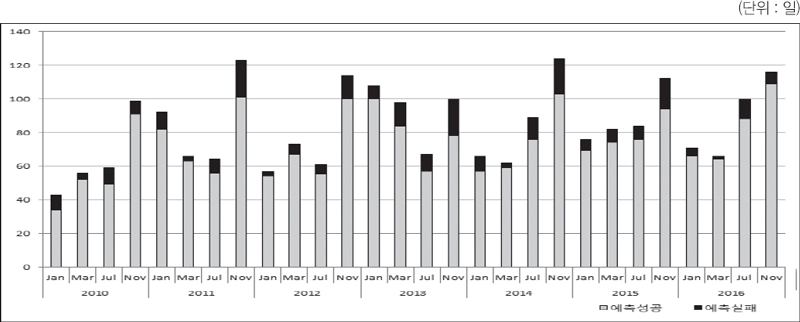
인터컨티넨탈(ICE) 선물거래소에서 2010년 이후 2016년까지 7년간 4개 계약월에 대해 분석하였다. 이전의 1982∼2000기간과 다른 점은 9월물 대신 7월물이 분석대상으로 교체되었고, 11월물, 1월물, 3월물, 7월물을 분석 대상으로 하였으며 4개 계약월에 대해 7년간 28회 판별분석을 하였다. ICE거래소에서 9월물 거래가 분석기간 중에 중단되어 7월물을 분석대상으로 하였다.

2010∼2016년 기간 동안 인터컨티넨탈 거래소에서 캐놀라 선물 일일 거래일은 7년 기간 동안 총 4,485일이며, 여기서 4,485일은 7년간 4개 계약월의 실질적인 거래일이다. 총 거래일 4,485일 중에서종장가격이 전일에 비해 하락한 일은 2,328일이며 상승한 경우는 2,117일, 가격 불변인 경우는 40일이다. 베이즈 판별분류법칙(DCR)은 2,026일을 가격 하락으로 분류를 하였고, 1,853일을 가격 상승으로, 그리고 가격 불변은 19일로 예측하였다. 이 기간 동안에도 종장가격이 전일 대비 불변인 경우는 매우 드믄 경우로 예측결과에 나타났다. 판별분류법칙은 가격 하락시 87.0%의 정확한 예측을, 가격 상승시 87.5%의 정확한 예측을 그리고 가격 불변시 47.5%의 예측력을 보였다.

<표 2>

모수 Bayes DCR에 의한 예측결과 종합(2010〜2016)

<그림 3>

모수 Bayes DCR에 의한 연도별 가격 하락 예측결과(2010〜2016)

<그림 4>

모수 Bayes DCR에 의한 연도별 가격 상승 예측결과(2010〜2016)

2. 비모수(Non-Parametric) 분석결과

1) 1982∼2000년 기간

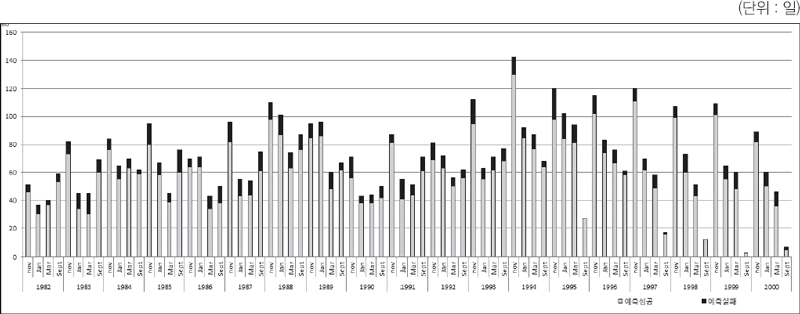
비모수 추정 판별분류법칙(Nonparametric Nearest Neighbor DCR)이 동일한 분석자료를 대상으로 적용되었다. 이들 19년 기간 동안 4개 계약월을 대상으로 한 판별분석이 이루어져 총 76회 비모수 추정 판별분석이 이루어졌다. 종합적으로 총 거래일 10,998일 중에서 종장가격이 전일에 비해 하락한 일은 5,543일이며 상승한 경우는 5,291일, 가격 불변인 경우는 183일이다. 비모수 추정 판별분류법칙은 4,836일을 가격 하락으로 분류를 하였고, 4,599일을 가격 상승으로, 그리고 가격 불변은 0일로 예측하였다. 비모수 추정의 경우도 종장가격이 전일 대비 불변인 경우는 예측결과가 좋지 않았다. 판별분류법칙은 가격 하락시 87.2%의 정확한 예측을, 가격 상승시 86.9%의 정확한 예측을 그리고 가격 불변시 0%의 예측력을 보였다 .

<표 3>

비모수 추정 DCR에 의한 예측결과 종합(1982-2010)

이상의 결과를 모수 추정치와 비교하면, 3월물에 대한 가격 하락 예측을 제외하고는 비모수추정치 결과에 차이가 있음을 알 수 있다. 가격이 불변일 경우 예측결과는 완전히 실제상황과 다르게 나타났다. 이는 가격 불변의 경우 최근접 이웃 그룹방법이 작동되지 않지만, 가격 하락시와 가격 상승시에는 여전히 높은 정확한 예측력을 보이고 있다.

<그림 5>

비모수 Nearest Neighbor DCR에 의한 연도별 가격 하락 예측결과(1982-2000)

<그림 6>

비모수 Nearest Neighbor DCR에 의한 연도별 가격 상승 예측결과(1982-2000)

2) 2010∼2016년 기간

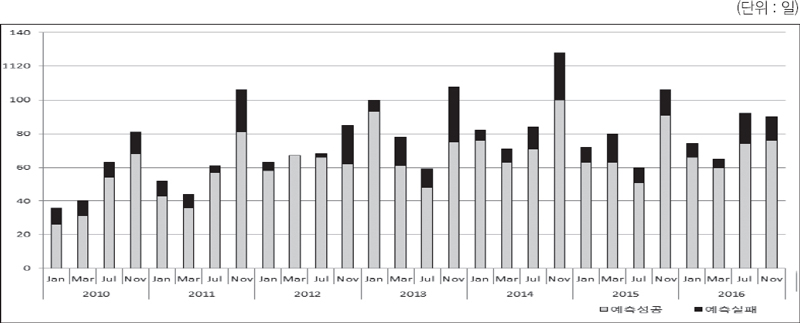
2010년∼2016년 기간 동안 총 거래일 4,485일 중에서 종장가격이 전일에 비해 하락한 일은 2,328일이며 상승한 경우는 2,117일, 가격 불변인 경우는 40일이다. 비모수 판별분류법칙(DCR)은 2,065일을 가격 하락으로 분류를 하였고, 1,780일을 가격 상승으로, 그리고 가격 불변은 5일로 예측하였다. 이 기간 동안에도 종장가격이 전일 대비 불변인 경우는 매우 드문 경우로 예측결과에 나타났다. 판별분류법칙은 가격 하락시 88.7%의 정확한 예측을, 가격 상승시 84.0%의 정확한 예측을 그리고 가격 불변시 12.5%의 예측력을 보였다.

<표 4>

비모수 Nearest Neighbor DCR에 의한 예측결과 종합(2010-2016)

<그림 7>

비모수 Nearest Neighbor DCR에 의한 연도별 가격 하락 예측결과(2010-2016)

<그림 8>

비모수 Nearest Neighbor DCR에 의한 연도별 가격 상승 예측결과(2010-2016)

3. 선물시장 효율성에 대한 가설검정

1) 1982∼2000년 기간

분석기간인 1982∼2000 기간 동안 4개 계약월에 대한 예측결과 가격이 하락한 경우 정확한 예측률은 86.1%에서 90.6%까지 나타났다. 1982∼2000년 기간 동안 가격 하락의 경우 11월물이 가장 높은 예측력을 가지고 있고 표준편차에서도 가장 작게 나타나 안정적인 거래행위를 보이고 있다. 동기간 동안 가격 상승의 경우 평균적으로 정확히 예측한 비율은 81.3%에서 89.6%로 나타나 계약월간의 편차가 가격 하락의 경우보다 크게 나타났다.

예측결과의 계약월과 연도에 따른 동질성에 대한 통계적 검정결과 모수 추정결과 가격이 상승한 경우 계약월에 따라, 그리고 가격이 하락한 경우의 연도에 따라 95% 신뢰구간에서 결과에 차이가 있는 것으로 나타났다. 모수 추정 시 가격 하락의 경우 연도별로 예측력에 차이가 있는 것으로 나타났지만, 계약월에 따라서는 차이가 없는 것으로 분석되었다. 즉, 가격이 상승할 경우는 계약월에 따라서 예측력이 다르게 나타나고, 가격이 하락할 경우 연도에 따라 결과에 차이가 있는 것으로 분석되었다.

비모수 추정결과에서는 가격 상승시 계약월에 따라서 예측력에 차이가 있는 반면 연도별로는 차이가 없는 것으로 분석되었다. 가격 하락시에는 계약월과 연도에 관계없이 예측력에 차이가 없는 것으로 나타났다. 즉, 가격이 상승할 경우는 계약월 선택에 따라 거래참여자들의 행위가 다르게 나타나지만, 가격 하락시에는 계약월에 관계없이 시장참여자들의 행위 패턴이 동일하게 나타남을 의미한다.

<표 5>

예측결과의 동질성에 관한 GLM 통계검정 결과(1982-2000)

2) 2010∼2016년 기간

모수추정의 경우 가격 하락 예측은 85.3%에서 87.9%를, 가격 상승은 85.7%에서 89.5%를 보여 상대적으로 높은 예측 능력을 보였다. 비모수추정의 경우 가격 하락은 85.7%에서 91.4%를, 가격 상승의 경우 78.5%에서 88.7%의 예측력을 보였다.

<표 6>

예측결과의 동질성에 관한 GLM 통계검정 결과(2010-2016)

예측결과의 동질성에 대한 통계적 검정결과 가격이 상승한 경우 95% 신뢰구간에서 모수추정과 비모수추정에 관계없이, 계약월과 연도에 관계없이 예측력에 차이가 없는 것으로 분석되었다. 즉, 가격이 상승할 경우에는 선물거래자들의 거래행위 패턴이 모수 또는 비모수 관계없이 일정하게 나타남을 의미한다. 그리고 가격이 하락한 경우 모수추정에서는 연도별로 예측력, 즉 거래행위자들의 거래패턴에 차이가 있으나, 계약월에 따라서는 예측력, 거래행위자들의 패턴에 차이가 없는 것으로 분석되었다. 가격 하락시 비모수 추정에서는 계약월과 연도에 관계없이 예측력에 차이가 없는 것으로 분석되었다. 즉, 가격 하락시 비모수 추정에서는 선물시장 참여자들의 거래행위가 유사하여 예측력에 차이가 없음을 나타낸다.

V. 결 론

본 연구에서는 다변량 분석법 중 판별분석법(discriminant analysis)이 일일 거래행위의 반복성에 의한 예측력을 판단하는데 응용되었다. 거래행위에 대한 예측력은 78%대에서 90%대 수준으로 높게 나타나, 캐놀라 선물시장에서 가격이 하락할 경우와 상승할 경우 거래행위에서 일정한 구조가 존재함을 보여주고 있다. 즉, 캐놀라 선물시장의 경우 시장이 비효율적이며 따라서 과거 데이터를 이용한 예측이 가능할 수 있음을 나타낸다. 계약월과 연도별 거래행위의 동질성 여부에 대한 통계분석결과는 95% 신뢰구간에서 가격 상승과 가격 하락시 서로 다르게 나타나고, 계약월과 연도별로, 그리고 모수분석과 비모수분석의 경우 결과가 다르게 나타났다.

1982∼2000년 기간의 경우 모수 추정의 경우가 비모수 추정의 경우보다 예측능력이 약간 높게 나타났으나, 2010년∼2016년 기간 동안에는 가격 하락시 비모수 추정치의 예측력이 높게 나타나 분석기간에 따라 예측력이 다를 수 있음을 보였다. 본 연구의 분석결과는 선행연구에서 제시한 선물시장에서의 시계열적 상관성과 함께 효율적인 예측력을 보여준 결과와 유사한 것으로 판단할 수 있다. 이러한 결과는 선물시장에서의 가격 변동은 시장참여자들의 행위의 결과이고 이러한 행위는 어느 정도 예측가능하다는 점을 부분적으로 증명하고 있다.

향후에는 캐놀라 종장가격의 방향과 시장행위, 시장가격, 거래량, 그리고 미청산계약고 간의 함수관계에 대한 추가적인 연구가 필요하고, 변수간 인과관계에 대한 명확한 해석도 필요하다. 단순히, 가격방향의 판별에서 가격상승, 가격불변, 가격하락의 방향만이 아닌 상승 또는 하락의 정도를 반영하여 가중치를 부과하고 일정 폭 이상의 변화가 있을 때 판별을 하도록 하는 방안을 향후 연구에서 시도할 수 있을 것이다.

끝으로, 캐놀라 이외의 타 농산물을 포함한 상품선물 및 금융선물에 적용시켜 시장행위의 패턴여부를 파악할 수 있을 것이다. 이상에서 제시한 한계에도 불구하고, 본 연구결과는 효율적인 예측도구로서 가격결정 시스템에 일정 구조가 존재하고, 시장참여자들의 거래행위가 반복될 때 기술적 분석이 가능하다는 점을 제시하였다는 점에서 그 의의를 찾을 수 있다.

Acknowledgments

본 논문은 경기연구원의 2017년 기본연구 결과인 「선물시장 거래자자의 행동패턴과 시장효율성」을 논문 형식으로 수정 보완한 자료임.

Notes

1) 캐놀라는 캐나다가 주산지인 유채의 일종이며, 식용이 어려운 유채를 식용이 용이하게 만든 변이종으로 1970년대에 캐나다에서 재배되기 시작했고 현재는 식용유 형태로 다양하게 활용되고 있다.

2) 2007년 9월, 위니펙거래소(WCE)가 ICE의 자회사가 되면서 명칭이 변경되었으며, 캐나다가 주산지인 캐놀라 선물거래가 가장 활발한 거래소이다.

3) 위니펙거래소(WCE)와 인터컨티낸털거래소(ICE)는 캐나다 마니토바주 위니펙시에 위치한 사실상 동일한 거래소로서, 운영주체와 명칭만 2007년 변경된 상태이다. 현재의 ICE 거래소는 캐놀라 선물거래가 가장 큰 규모로 거래되고 있는 주산지의 선물시장으로서, 거래물량과 캐놀라 가격을 선도하는 대표성이 있는 캐놀라 선물시장이다.

References

이상훈·정윤경(2017), 『선물시장 거래자의 행동패턴과 시장효율성』, 경기연구원 기본연구 2017-1
Bessler & Covey(1991), “Cointegration: some results on U.S. cattle prices”, The Journal of Futures Market, 461-471. [https://doi.org/10.1002/fut.3990110406]
Bosch & Pradkhan(2016), “Trading Activity and rate of Convergence in Commodity Futures Markets”, The Journal of Futures Market, 1-9. [https://doi.org/10.1002/fut.21831]
Chowdhury(1991), “Futures market efficiency: evidence from cointegration tests”, The Journal of Futures Market, 577-589. [https://doi.org/10.1002/fut.3990110506]
Corazza, Malliaris, & Nardelli(1997), “Searching for fractal structure in agricultural futures markets”, The Journal of Futures Market, 17(4), 433-473. [https://doi.org/10.1002/(SICI)1096-9934(199706)17:4<433::AID-FUT4>3.0.CO;2-I]
DeCoster, Labys, & Michell(1992), “Evidence of chaos in commodity futures prices”, The Journal of Futures Market, 12(3). 291-305. [https://doi.org/10.1002/fut.3990120305]
Goldenberg(1989), “Memory and equilibrium futures prices”, The Journal of Futures Market, 577-589.
Helms, Kaen, & Rosenman(1984), “Memory in commodity futures contracts”, The Journal of Futures Market, 4(4), 559-567. [https://doi.org/10.1002/fut.3990040408]
Jiang & Tian(2011), “A Random walk down the options market”, The Journal of Futures Market, 32(6), 505-535. [https://doi.org/10.1002/fut.20528]
Johnson(1998), Applied Multivariate Methods for Data Analysis, DuxvuryPress [https://doi.org/10.2307/2533879]
Kamara(1982), “Issues in futures markets: a survey”. The Journal of Futures Market, 2(3), 261-294. [https://doi.org/10.1002/fut.3990020306]
Kawaller, Koch, & Peterson(1994), “Assessing the intraday relationship between implied and historical volatility”, The Journal of Futures market, 14(3), 323-346. [https://doi.org/10.1002/fut.3990140306]
Martel & Trevino(1990), “The intraday behavior of commodity futures prices”, The Journal of Futures Market, 10(6), 661-671. [https://doi.org/10.1002/fut.3990100608]
Morrison(2004), Multivariate Statistical Methods, 4th Edition, Thomson Brooks/Cole, New York.
Olszewski(1998), “Assessing inefficiency in the futures markets”, The Journal of Futures markets, 18(6), 671-704. [https://doi.org/10.1002/(SICI)1096-9934(199809)18:6<671::AID-FUT3>3.0.CO;2-1]
Schroeder & Goodwin(1991), “Price discovery and cointegration for live hogs”, The Journal of Futures Market, 685-696. [https://doi.org/10.1002/fut.3990110604]
Westerlund, Norkute, & Narayan(2014), “A factor analytical approach to the efficient futures market hypothesis”, Performance of Financial Markets and Credit Derivatives, Deakin University, Australia. [https://doi.org/10.1002/fut.21687]

이상훈 Lsh129@gri.kr

1994년 미국 Mississippi State University에서 경제학 박사학위를 받았다. 경기연구원 경제사회연구부장, 기획조정실장, 부원장, (사)한국지역경제학회 이사, (사)한국파생상품시장연구회 회장을 역임하였고, 현재 경기연구원 상생경제연구실 선임연구위원으로 재직 중이다. 저술은 공저로 「파생상품시장의 발전과 모색」(한나래플러스 2011) 등이 있다. 주요 전문분야는 선물옵션시장에 대한 기술적분석이고, 회귀분석 외에 다변량분석법, 비모수분석, 수리계획모형, 비용편익분석, 투입산출모형 등 계량분석기법을 다양한 실물분야에 응용하는데 관심이 있다.

계약월	가격 하락 예측/실제일(%)	가격 상승 예측/실제일(%)	가격 불변 예측/실제일(%)	계(일)
Jan.	1,186/1,377(86.1)	1,132/1,294(87.5)	1/40 (2.5)	2,691
Mar.	1,076/1,213(88.7)	924/1,137(81.3)	6/48 (12.5)	2,398
Sept.	960/1,083(88.6)	902/1,007(89.6)	1/38 (2.6)	2,128
Nov.	1,695/1,870(90.6)	1,655/1,853(89.3)	0/57(0.0)	3,781
계	4,917/5,543(88.7)	4,613/5,291(87.2)	8/183(4.4)	10,998

계약월	가격 하락 예측/실제일(%)	가격 상승 예측/실제일(%)	가격 불변 예측/실제일(%)	계(일)
Jan.	451/513(87.9)	417/479(87.0)	0/5(0.0)	997
Mar.	441/503(87.6)	396/447(88.5)	2/6(6.7)	956
Jul.	447/524(85.3)	436/487(89.5)	2/10(20.0)	1,021
Nov.	687/788(87.1)	604/704(85.7)	15/19(78.9)	1,511
계	2,026/2,328(87.0)	1,853/2,117(87.5)	19/40(47.5)	4,485

계약월	가격 하락 예측/실제일(%)	가격 상승 예측/실제일(%)	가격일정 예측/실제일(%)	계(일)
Jan.	1,195/1,377(86.8)	1,106/1,294(85.5)	0/40(0.0)	2,691
Mar.	1,050/1,213(86.6)	966/1,137(84.0)	0/48(0.0)	2,398
Sept.	957/1,083(88.4)	889/1,007(88.3)	0/38(0.0)	2,128
Nov.	1,634/1,870(87.4)	1,638/1,853(88.3)	0/57(0.0)	3,781
계	4,836/5,543(87.2)	4,599/5,291(86.9)	0/183(0.0)	10,998

계약월	가격 하락 예측/실제일(%)	가격 상승 예측/실제일(%)	가격 불변 예측/실제일(%)	계(일)
Jan.	469/513(91.4)	425/479(88.7)	2/5 (40.0)	997
Mar.	463/503(92.0)	381/447(85.2)	1/6 (16.6)	956
Jul.	457/524(87.2)	421/487(86.4)	1/10 (10.0)	1,021
Nov.	676/788(85.7)	553/704(78.5)	1/19 (5.2)	1,511
계	2,065/2,328(88.7)	1,780/2,117(84.0)	5/40 (12.5)	4,485

	가격 상승		가격 하락
	계약월(contracts)	연도(year)	계약월(contracts)	연도(year)
모수추정결과	p=<0.0001	p=0.0973	p=0.6441	p=0.0428
비모수추정결과	p=0.0366	p=0.2526	p=0.4212	p=0.44450